MRO in Python Programming

OOPs in Python

What is MRO in Python?

The MRO in python stands for Method Resolution Order, a set of rules for searching methods for execution in an inheritance hierarchy. It searches the methods in an inheritance hierarchy from bottom to top and from left to right order.

According to MRO, there are three rules for searching methods in an inheritance hierarchy, and they are:

• In single or multilevel inheritance, the method is searched first in the sub-class before going to its base class. For example, if class B inherits class A, the MRO will search for the methods in class B first and, if not found, will go to search for methods in class A.
• In multiple inheritance, the methods are first searched in the sub-class and then in the order from left to right in the base class. For example, if class C inherits class A and B, it will search in class C, then in class A and then in class B.
• The last rule is that it will not visit any class more than once in an inheritance hierarchy.

Note: To display the complete MRO of a class, we can use the method mro().

Let's see some examples that show the implementation of the above rules.

class A:
    def display(self):
        print('In Class A')

class B(A):
    def show(self):
        print('In Class B')


x = B()
x.display()

# Display MRO of Class B
print(B.mro())

In Class A
[<class '__main__.B'>, <class '__main__.A'>, <class 'object'>]

The complete MRO of ClassB will be B -> A -> object

In the above example, we can see the MRO of class B. That means, if we call a method using the object of class B, then the python interpreter will search the method in class B first. If not found, it will search the method in class A and then in the object class.

class A:
    def display_x(self):
        print('In Class A')

class B(A):
    def display_y(self):
        print('In Class B')

class C(B):
    def display_z(self):
        print('In Class C')


x = C()
x.display_x()

# Display MRO of Class C
print(C.mro())

In Class A
[<class '__main__.C'>, <class '__main__.B'>, <class '__main__.A'>, <class 'object'>]

The complete MRO of ClassC will be C -> B -> A -> object

class A:
    def display_a(self):
        print('In Class A')

class B:
    def display_b(self):
        print('In Class B')

class C:
    def display_c(self):
        print('In Class C')

class X(A, B):
    def display_x(self):
        print('In Class X')

class Y(B, C):
    def display_y(self):
        print('In Class Y')

class Z(X, Y, C):
    def display_z(self):
        print('In Class Z')



x = Z()
x.display_a()

# Display MRO of Class Z
print(Z.mro())

In Class A
[<class '__main__.Z'>, <class '__main__.X'>, <class '__main__.A'>, <class '__main__.Y'>, <class '__main__.B'>, <class '__main__.C'>, <class 'object'>]

The complete MRO of ClassZ will be Z -> X -> A -> Y -> B -> C -> object

As per the third rule of MRO, no class will be visited more than once in an inheritance hierarchy. So ClassB is visited only once as per MRO in multiple inheritance, as shown in the above output.

How Python Creates MRO List from Inheritance

Python uses the C3 Linearization algorithm to create the MRO list from an inheritance. The algorithm follows the divide and conquers rule to calculate the Method Resolution Order list of an inheritance.

For example, if class A inherits the base classes B, C, and D. The MRO list of class A will be calculated as the sum of class A plus merging the list of parents of the base classes and the base classes itself as shown below.

We can calculate the MRO list of class A as A + merge(L[B], L[C], L[D], BCD). Here L[B] means the linearization of class B, which includes all the base classes of class B.

Let's find out the MRO of the above-given example 3 manually.

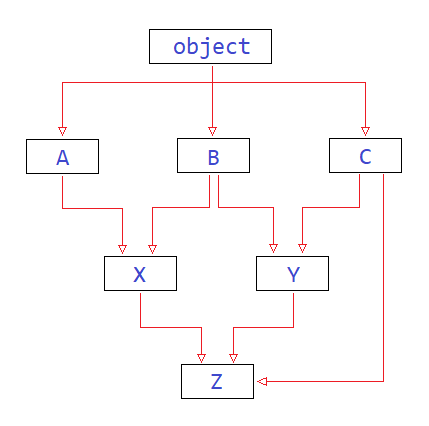
The MRO of class Z will be calculated as Z + merge(L[X], L[Y], L[C], XYC).

Using the divide and conquers rule first, we will find the linearization of class X, which can be calculated as L[X] = X + merge(L[A], L[B], AB).

L[X] = X + merge(L[A], L[B], AB)
= X + merge(AO, BO, AB)       A is a good head because it appears in the first position in AO and AB, so add it to the list and remove it from the merge list.
= X + A + merge(O, BO, B)     O is not a good head because it appears in the second position in BO, so skip it and read the next head, B, which is a good head, so add it to the list and remove it from the merge list.
= X + A + B + merge(O, O)     Now O is a good head, add it to the list and remove it from the merge list.
= X + A + B + O               so the final linearization of X is
= X A B O

If a class does not inherit any other class, then its default parent class will always be the object class. In the above explanation, the O means the object class, the default parent class of classes A, B, and C, as shown in the image above.

The linearization of class Y will be calculated as L[Y] = Y + merge(L[B], L[C], BC).

L[Y] = Y + merge(L[B], L[C], BC)
= Y + merge(BO, CO, BC)       B is a good head. Add it to the list and remove it from the merge list.
= Y + B + merge(O, CO, C)     C is a good head, so add it to the list and remove it from the merge list.
= Y + B + C + merge(O, O)     Now O is a good head, add it to the list and remove it from the merge list
= Y + B + C + O               so the final linearization of Y is
= Y B C O

The linearization of class C will be CO because class C does not inherit any other class, so its parent class will be the object class.

We have calculated the linearization of classes X, Y and C. We will combine them all to find the linearization of class Z.

L[Z] = Z + merge(L[X], L[Y], L[C], XYC)
= Z + merge(XABO, YBCO, CO, XYC)            X is a good head. Add it to the list and remove it from the merge list.
= Z + X merge(ABO, YBCO, CO, YC)            A is a good head. Add it to the list and remove it from the merge list.
= Z + X + A + merge(BO, YBCO, CO, YC)       B is not a good head, so skip it. Y is a good head so add it to the list and remove it from the merge list.
= Z + X + A + Y + merge(BO, BCO, CO, C)     Now B is a good head, add it to the list and remove it from the merge list
= Z + X + A + Y + B + merge(O, CO, CO, C)   O is not a good head, so skip it. C is a good head so add it to the list and remove it from the merge list.
= Z + X + A + Y + B + C + merge(O, O, O)    Now O is a good head, add it to the list and remove it from the merge list
= Z + X + A + Y + B + C + 0                 so the final linearization of Z is
= Z X A Y B C O